Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 스프링시큐리티
- springdataredis
- Spring
- 메시지
- AWS
- java
- JIRA
- yaml-resource-bundle
- 스프링부트
- 파이썬
- 도커
- 액세스토큰
- springsecurityoauth2client
- CI/CD
- 국제화
- 오블완
- githubactions
- oauth2
- 백준
- docker
- springsecurity
- 트랜잭션
- 스프링
- 소셜로그인
- 티스토리챌린지
- 리프레시토큰
- 프로그래머스
- 데이터베이스
- 재갱신
- 토이프로젝트
Archives
- Today
- Total
땃쥐네
[CS] 혼공컴운 - 2.1 0과 1로 숫자를 표현하는 방법 본문
이 글은
- '강민철'님의 책 '혼자 공부하는 컴퓨터구조 + 운영체제' 책을 읽으며 학습한 내용을 정리합니다.
1. 정보단위 : 비트, 바이트, ...
1.1 비트

- 0 과 1을 나타내는 가장 작은 정보 단위
- 1비트는 2가지 정보를 표현할 수 있다.
- 2비트는 2**2 가지 정보를 표현할 수 있다.
- n비트는 2**n 가지 정보를 표현할 수 있다.
1개의 비트를 통해 2가지 정보를 표현할 수 있고, 이를 확장하여 여러 개의 비트를 통해 다양한 정보를 표현할 수 있게 된다.
1.2 비트의 묶음
- 바이트 : 1byte == 8bit
- 킬로바이트(KB, Kilobyte) : 10**3(==1000) byte
- 메가바이트(MB, Megabyte) : 10**6 byte == 1000 KB
- 기가바이트(GB, Gigabyte) : 10**9byte == 1000 MB
- 테라바이트(TB, Terabyte) : 10**12byte == 1000 GB
1.3 (참고) 이진 바이트 표기법
- 바이트 : 1byte == 8bit
- 키비바이트(KiB, Kibibyte) : 2**10 (== 1024) byte
- 메비바이트(MiB, Mebibyte) : 2**20 byte
- 기비바이트(GiB, Gibibyte) : 2**30 byte
- 테비바이트(TiB, Tebibyte) : 2**40 byte
나 역시 이 책을 읽기 전까지는 1kb가 1024 byte인 줄 알고 있었는데, 이 책을 읽고나서 이진 바이트 표기법과 십진 바이트 표기법을 구분해야 한다는 것을 알게 됐다.
우리가 하드디스크를 구입하면, Windows 기준으로 HDD의 최대 용량이 작아보이는데 하드디스크 제품들의 바이트 표기법은 십진 표기법을 기준으로 판매되고 Windows에서의 용량 표기법은 이진법을 기준으로 하기 때문이다.
예를 들어 1TB SSD를 하나 구매하고 Windows 기반 컴퓨터에 연결하면 "931GB"로 표시된다. 된다. 1TB를 이진 바이트 표기법으로 환산하면 1TiB보다 93기비바이트 정도 모자라게 되는데 1024GiB-93=931GiB가 되는 것이다. 문맥에 따라 기비바이트를 기가바이트로 표기하는 곳도 있기 때문에 각각의 문맥을 잘 읽어야한다.
1.4 다른 표현법
- 니블(Nibble) : 4bit (1바이트의 절반)
- 워드(Word)
- CPU가 한 번에 처리할 수 있는 데이터 크기
- CPU가 한 번에 16비트를 처리할 수 있다면, 1워드는 16비트가 되고, 32비트를 처리할 수 있다면 1워드는 32비트가 된다.
- 2022년 기준, 컴퓨터의 워드 크기는 보통 32비트 혹은 64비트가 된다.
- 하프 워드(Halfword) : 워드의 절 반 크기
- 더블 워드(Doubleword) : 워드의 두 배 크기
그렇게 자주 쓰이는 표기법은 아니라서 몰라도 된다.
2. 이진법
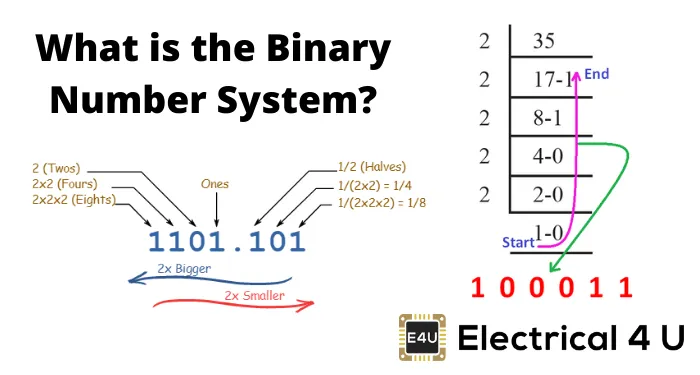
2.1 이진법 : 0과 1만으로 모든 숫자를 표현하는 방법
- 0과 1만으로 모든 숫자를 표현하는 방법
- 비트의 갯수는 표현할 수 있는 값의 범위를 결정한다.
- 다른 진법과 구분하기 위해 앞에 '0b' 를 붙여서 사용한다.
- 예) 0b1000 == 16, 0b0101 == 5
2.2 이진수의 음수 표현

- 2의 보수법 : 더했을 때, 자리 올림이 발생하여 0이 되는 수를 2의 보수라고 한다. 양수의 2의 보수를 음수로 처리하는 기법.
- 쉽게 2의 보수 얻어내는 법 : 1의 보수(모든 비트에 NOT연산. 더했을 때 모든 비트가 1이 되는 수)에 1을 더한 값이 2의 보수가 된다.
- 실제 2진수를 다룰 때는, 양수인지 음수인지 구분하기 위해 플래그(flag)를 사용하기 때문에, 컴퓨터가 부호를 헷갈릴 일이 없다고 함.
플래그에 관한 내용은 뒤의 4장에서 다룬다.
3) 십육진법

3.1 십육진법
- 한 자리에 0~15의 값을 표현할 수 있는 진법
- 15를 넘어가는 시점(16) 시점에, 자리를 올림하여 수를 표현한다.
- 십진수 10, 11, 12, 13, 14, 15를 A,B,C,D,E,F 로 표기한다.
- 다른 진법과 구분하기 위해 컴퓨터에서는 앞에 '0x'를 붙여 사용한다.
3.2 더 작은 자릿수로 더 많은 정보를 표현할 수 있다.
- 십진수 32를 이진법으로 표기하면 0b100000 인데, 무려 6개의 자릿수가 필요하다.
- 십진수 32를 십육진법으로 표기하면 0x20으로, 두개의 자릿수만 필요하다.
3.3 이진수, 십육진수 간 변환이 매우 편리하다.
- 십육진수를 이진수로 변환하기 : 십육진수 한 글자를 4비트의 이진수로 간주하여 변환한다.
- 예) 0x1A1B -> 0001 1010 0010 1011 -> 0b0001101000101011
- 이진수를 십육진수로 변환하기 : 이진수 숫자를 4개씩 끊고, 각각 십육진수로 변환하여 붙여주면 된다.
- 예) 0b11010101 -> 1101 0101 -> D 5 -> 0xD5
- 이러한 변환이 매우 편리하기 때문에 주로 데이터를 표기할 때 십육진수로 묶어서 많이 표현한다.
'CS > Computer Structure' 카테고리의 다른 글
| [CS] 혼공컴운 - 3.2 명령어의 구조 (0) | 2023.01.15 |
|---|---|
| [CS] 혼공컴운 - 3.1 소스 코드와 명령어 (2) | 2023.01.13 |
| [CS] 혼공컴운 - 2.2 0과 1로 문자를 표현하는 방법 (0) | 2022.12.18 |
| [CS] 혼공컴운 - 1.2 컴퓨터 구조의 큰 그림 (0) | 2022.12.18 |
| [CS] 혼공컴운 - 1.1 컴퓨터 구조를 알아야 하는 이유 (0) | 2022.12.18 |
Comments




